日刊Coroutines(2) あとはやるだけ(終)

1. はじめに

あけおめ､びしょ～じょです｡では前回からの続きです｡ 構文を定義したのであとは評価器を実装するだけです｡

そういえば前回オキャモーを書いてましたが全体はこちらにあります｡

GitHub - Nymphium/lambda-c: lambda calculus + coroutines

lambda calculus + coroutines. Contribute to Nymphium/lambda-c development by creating an account on GitHub.

2. 構文ふえる

といきたかったのですが構文が増えます｡

構文はこんなかんじに拡張されました

v ::= ... | l | nil
t ::= ... | l:e

ソースのほう

type t =
+  | Nil
   | Int of int
   | Var of string
   | Let of string * t * t
@@ -8,3 +9,5 @@
   | Create of t
   | Resume of t * t
   | Yield of t
+  | Label of string
+  | LabelE of string * t

基本的に評価時都合のものです｡ 話を先取りすると､コルーチンは値ではなく参照を持ちたい｡ なのでラベルlを用いてコルーチンを指します｡ l:eはラベル式と呼び､ラベルlの指すコルーチンにおり､eを評価するという感じ｡ nilはその参照の初期化に使います｡ぶっちゃけなくてもいい｡

2-1. Builder の変更

関数を作るBuilder.fnが間違ってました｡ とか構文追加に伴うアレソレとか｡

+  let nil = Nil
   let int v = Int v
   let var x = Var x

   let fn f : t =
-    let x = var @@ gensym () in
-    f x
+    let x = gensym () in
+    Fun (x, f @@ var x)
   ;;

   let ( let@ ) v k =
@@ -34,10 +38,42 @@
     Let (x, v, k @@ var x)
     ;;
   (* List.append とぶつかるとエラーメッセージが分かりづらいんじゃなあ *)
-  let ( @ ) f a = App (f, a)
+  let ( <@> ) f a = App (f, a)
   let prim s = PrimOp s
+  let ( <+> ) l r = prim "+" <@> l <@> r
+  let ( <-> ) l r = prim "-" <@> l <@> r
   let create f = Create f
   let resume co a = Resume (co, a)
   let yield v = Yield v
+  let label s = Label s
+  let labelE l e = LabelE (l, e)

値の話もちゃっかりここでやっておく｡

let is_value = function
  (* 変数は実際の値に置き換えられ､評価時に都合が悪いので除いた *)
  | Nil | Int _ | Fun _ | Label _ -> true
  | _ -> false

3. 意味論

[1]の図3.7を参照のこと｡ 今回は再帰がないので \(\textrm{L{\small et}R{\small ec}}\) 規則は除く｡ 図3.8もパターンマッチングに関するものなので無視シャス｡ そしてなんとミスを見つけました!!!! \(\textrm{L{\small et}}\) 規則の左辺と右辺で prime があったりなかったりします!!!!!

3-1. 評価文脈

ところで C[] とは何だ? これは evaluation context です｡ まぁコールスタックというか継続みたいなもんですね｡

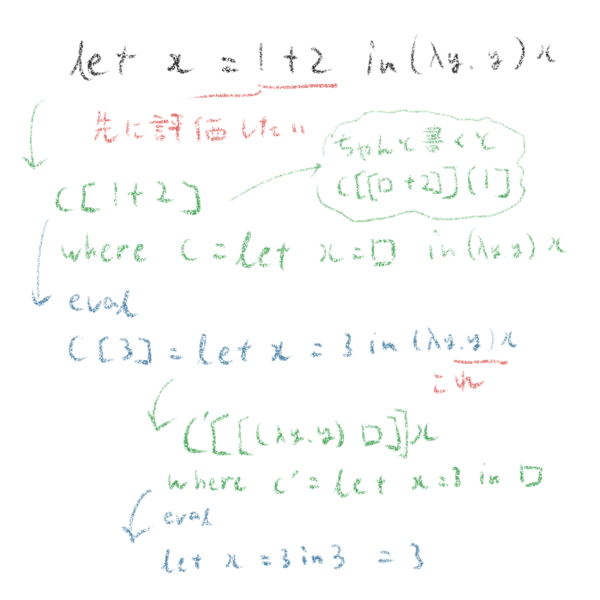図3.1. 超図解 評価文脈

ある項から､評価文脈と評価したい項(というか評価文脈が[ ]なる項､つまり値)を分離する関数punchを定義する｡ ガボッとやるのでpunchです｡慣習などではない｡

(** create evaluation context; always left-to-right *)
(** t -> t', C *)
let rec punch : Syntax.t -> Syntax.t * (Syntax.t -> Syntax.t) = function
  | Let (x, bnd, body) when not @@ is_value bnd ->
    let bnd', c = punch bnd in
    bnd', fun hole -> Let (x, c hole, body)
  (* binary operators *)
  (* C op r *)
  | App (App ((PrimOp _ as op), l), r) when not @@ is_value l ->
    let l', c = punch l in
    l', fun hole -> App (App (op, c hole), r)
  (* v op C *)
  | App (App ((PrimOp _ as op), l), r) when not @@ is_value r ->
    let r', c = punch r in
    r', fun hole -> App (App (op, l), c hole)
    (* avoid to be recognized as usual function application *)
  | App (App (PrimOp _, l), r) as t when is_value l && is_value r -> t, Fun.id
  | App (f, e) when not @@ is_value f ->
    let f', c = punch f in
    f', fun hole -> App (c hole, e)
  | Create t when not @@ is_value t ->
    let t', c = punch t in
    t', fun hole -> Create (c hole)
  | Resume (l, e) when not @@ is_value l ->
    let l', c = punch l in
    l', fun hole -> Resume (c hole, e)
  | Yield e when not @@ is_value e ->
    let e', c = punch e in
    e', fun hole -> Yield (c hole)
  (* don't punch `labelE` to avoid `Yield` to be "top-level" *)
  (* t -> t, [ ] *)
  | other -> other, Fun.id

subterms がある項は､常に左側から評価を進めたいので､必ず左側から穴をあけていきます｡ 評価したい subterm がまだ値でない場合､さらに再帰的に punch していき､ hole に context を適用することで evaluation context を重ねていきます｡ そして､ subterms のうち1つだけ値でないものがある場合はそこで打ち切ります｡ というのも､意味論が小ステップなのでそんなに細かく文脈区切っても意味ないんですね｡

[1]ではラベル式も評価文脈を分解できるのですが､実際に実装してみるとここでは分解しないほうが良いということに気づきました｡ コメントにもあるとおり､ここでラベル式の subterm に潜ってしまうとyieldをうまく評価できないんですねぇ｡ 評価器の実装でもう一度触れます｡ こういったアハ体験があると初めて実装してよかったなと思いますね｡

3-2. ストア

変数とかラベルを保持しておくのに使います｡ [1]上の\(\theta\)です｡

(**
  * environment θ for variables and labels
  * each variables / labels is unique and global
  *)
module Store = struct
  open struct
    module M = Map.Make ((String : Map.OrderedType))

    let s : t M.t ref = ref M.empty
  end

  (** θ(x) *)
  let get x = M.find x !s

  (** θ[x <- v] *)
  let set x v = s := M.add x v !s

  (** θ[x <- nil *)
  let flush x = s := M.add x Nil !s

  (* for repl *)
  let reflesh () = s := M.empty
end

評価器を小ステップで実装する都合上､(term * env) -> (term * env)という型にすると毎回 tuple を deconstruct するのがめんどいんで全部グローバルにしました｡ 特にコルーチンは状態の更新が必要なため､よくある environment の型 (string, t) list とは違い mutable な map にしていますが､変数の代入は構文上も用意されておらず､やりません｡

オッこのMと ref cell をモジュール外から見えないようにするテクは先日書いたやつにあったな｡

3-3. 評価器

あとはやるだけ

let rec eval t =
  if is_value t
  then t
  else (
    let t', ctx = punch t in
    eval1 t' |> ctx |> eval)
and eval1 = function
  | (Int _ | Fun _ | Nil) as i -> i
  | Var x | Label x -> Store.get x
  | App (Fun (x, body), e) ->
    let () = Store.set x e in
    body
  (* binary-operation form: l token r = ((token l) r) *)
  | App (App (PrimOp token, l), r) -> binop token l r
  | Let (x, bnd, body) ->
    let () = Store.set x bnd in
    body
  | Create f ->
    let l = genlabel () in
    let () = Store.set l @@ f in
    Label l
  | Resume (Label l, e) ->
    let f = Store.get l in
    let () = Store.flush l in
    Builder.(labelE l (f <@> e))
  | Resume (l, _) -> failwith @@ Printf.sprintf "%s is not a label" @@ show l
  | LabelE (l, e) ->
    (* C[l:e] ~~> C[l:C'[e']] *)
    let e', c = punch e in
    (match e' with
    | Yield v (* v can be a value *) ->
      let x = gensym () in
      let () = Store.set l @@ Fun (x, c @@ Builder.var x) in
      v
    | v when is_value v -> v
    | other -> LabelE (l, c @@ eval1 other))
  | Yield _ -> failwith "yield from top-level is not allowed"
  | (App _ | PrimOp _) as inv ->
    failwith @@ Printf.sprintf "invalid term %s" @@ show inv

アレ?! eval1 はワンステップなのに recursive なんですか? まあちょっと待っててください説明しますんで｡ だいたいは意味論の通りにやっていきます｡ ガーッと評価してくれる evalを見ていただくと､ここで評価対象の term tを evaluation context と更に対象の subterm に分離して､その subterm を評価します｡ 評価したら､また evaluation context に評価された項をはめ直して再評価します｡ ｢はめ直したらダメじゃない?｣と一瞬思うんですが､例えばlet x = e in e'を punch してe, let x = [] in e'にしてからe ~> vになったらe'[x/v]を評価したくなるわけですね｡ というときにはめ直し操作が必要になります｡ binopは適当な2引数関数(または二項演算子)を表すトークン(文字列)からSyntax.t -> Syntax.t -> Syntax.tを返す関数です｡

3-3-1. コルーチンに関する操作

Createは関数を受け取ってコルーチンを生成し､それを指すラベルを返します｡ 再度申しますと､コルーチンは resume するたびに状態が更新されていくので､値ではなく参照がホシイわけですね｡なのでその参照を指すラベルを返す｡

Resumeはラベルと項を受け取って､項をそのラベルの指すコルーチンに渡して走らせます｡ 実際はラベルlと項eを受け取ってラベル式l:(θ[l] e)にします｡ コルーチンは引数を受け取ることから関数のようなインタフェースを持ってることが分かりますね｡ まぁ実際関数です｡ コルーチンlを呼んでる中でさらにlを呼ぶとぶっ壊れるので､ストア内のlを flush してます｡ ちょっとしたミソですね｡

さて散々引っ張ったラベル式labelEの解説です｡ その前に punch でlabelE(l, e)のeに潜らない話ですが､なんとなく察した方もいるかもしれません｡ labelEの評価時に先んじて punch してしまうと､その中にある(かもしれない)Yieldを評価してしまいます｡ そしてYieldを評価してコルーチンをぬけたい､となったときにそのリターンポイントが無いので書きようがない､となってしまいます｡ CEK マシンで意味論を定義するにもラベルに対応した部分の frame を取得するのはだいぶ難易度が高そうです｡ 実装は～ (label * Syntax.t -> Syntax.t) みたいな map でなんとかなるかもしれない｡型がないことに甘えてますねぇ!

…なのですぐには punch しません｡ 意味論の定義でも､ラベル式だけ evaluation context の構造を inspect する必要があるためだいぶ罠です｡ この罠を実感できるのが実際に紙(紙ではないが…)からプログラムにおこすところの味わいですね｡

さて punch しない理由がつかめたところで実装見てみましょう｡ とはいえすぐに punch します｡ これはlabelEの評価という文脈(!)が分かっているので punch できるわけですね｡ punch した結果Yield vが次に評価する項だった場合､ラベルの指すコルーチンの状態を更新します｡ これはまんま関数ですね｡evaluation context を関数にして放り込んでます｡ punch の結果が値だった場合は､ラベル式を抜けその値を返します｡ Yield の引数がまだ評価できる subterm だった場合は先にそちらを評価することになります｡ そういった場合も含め､新たにラベル式を作るようにします｡ このとき評価は1回進めたいのでeval1を呼んでます｡ ただ呼んだeval1は一度しか評価しないか､連続するlabelEを無限に潜っていくかになります｡ とはいえ後者の場合も結局は最終的に到達するlabelEではない subterm を一度評価して終わるので､やはり1ステップだけ評価が進むことになります｡ 辻褄あってますね｡

Yield単体の評価はすなわちコルーチンの外で呼ばれるものなので､ランタイムエラーとします｡

---

いい感じじゃないでしょうか｡ 動かしてみましょう｡

utop # open Lib;;
utop # let program =
  let open Syntax.Builder in
  let@ x = int 3 in
  let@ y = int 5 in
  let@ co = create @@ fn @@ fun x' ->
    let@ z = x <+> x' <+> y in
    let@ r = yield (z <+> int 7) in
    r
  in
  let@ r (* z + 7 が返ってくる *)  = resume co @@ int 2 (* [x'(co)/2] *) in
  let@ r' = resume co @@ r <+> int 4 (* [r(co)/r + 4] *) in
  r';;
val program : Syntax.t =
  (... 長い syntax tree が見られる)
utop # Lib.eval program;;
- : Syntax.t = Lib__.Syntax.Int 21

オッいい感じじゃないでしょうか｡ DSL も相まってわかりやすい(自画自賛)｡

4. おわりに

ウーン実装もかんたんだったな(10h弱)｡ ただ実装しないとわからないことがあったのは面白いです｡ あんまり深みないんですが終わりです｡ ありがとうございました｡ 本ブログでも再三再四触れていますが､[1]の\(\lambda_{\rm ac}\)の意味論を考えるにあたりベースにした論文[2]も面白いので読んでみてください｡

---

1. 河原悟 『コルーチンを用いた代数的効果の新しい実装方法の提案』 (令和元年度 筑波大学大学院 博士課程 システム情報工学研究科 修士論文) ↩

2. Moura, Ana Lúcia De, and Roberto Ierusalimschy. "Revisiting coroutines." ACM Transactions on Programming Languages and Systems (TOPLAS) 31.2 (2009): 6. ↩